행렬
- 행렬은 벡터를 나열한 것이다
단위행렬
- 벡터를 전혀 움직이지 않는 행렬
- 좌측상단 부터 우측 하단의 대각선상 성분이 모두 1 (m00,m11,m22) 이고 나머지는 0
신축행렬
- m00(x),m11(y),m22(z)
- 대각선 요소들이 x,y,z,
회전행렬
- 크기는 바꾸지 않고 방향만 바꾸는 행렬
- 코싸싸코
- y축 회전만 - 주는 것이 다르다
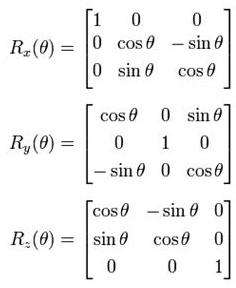
이동행렬
- 벡터에 덧셈을 하는 행렬
- 좌표가 이동

역행렬

1. 역 행렬(Inverse Matrix) 이란?
A-1A = AA-1 = I를 만족하는 A-1 - 즉, AB = BA = I일때 B는 A의 역행렬 .
(단, A,B는 n x n 정방행렬, I는 n x n 단위행렬)
2. 역행렬을 구해야하는 주요 이유
ㅇ 선형연립방정식 A x = b의 해 x = b A-1를 구할 필요가 있음
3. 역행렬을 구하는 방법들 ㅇ A x = I로부터 직접 푸는 방법

ㅇ 행렬식 이용 방법
- 행렬식과 크래머공식을 이용하여 구함

. adj A : 수반행렬(Adjoint Matrix)
. det A : 행렬식(Determinant)
4. 역 행렬의 존재 여부
※ ☞ 가역행렬 참조
- 역행렬 존재 => 가역행렬
- 역행렬 존재하지 않음 => 특이행렬

행렬의 곱셈 순서
* S(신축) X R(회전) X T(이동)
* 순서를 바꾸면 결과값이 달라짐.
'수학' 카테고리의 다른 글
| 게임수학 개요 (0) | 2021.05.25 |
|---|---|
| 지수,로그 + 지수함수,로그함수 (0) | 2019.06.04 |
| 사원수 회전을 행렬로 (0) | 2019.05.01 |
| 사원수 (0) | 2019.05.01 |
| 벡터 (0) | 2019.05.01 |