벡터
- 방향과 크기를 가지는 것
벡터의 크기
- 벡터의 크기 표시 : l l 를 붙여준다. ex) lAl
- 3차원 a벡터일 경우
$$ ㅣaㅣ= \sqrt{ax^2+ay^2+az^2}$$
스칼라
- 크기만 가지는 양
- ex) 두 벡터의 내적 결과는 스칼라
단위벡터
- ex=(1,0,0) , ey=(0,1,0), ez(0,0,1)
- 위처럼 크기가 1인 벡터를 단위 벡터, 혹은 정규화된 벡터라고 한다
기저벡터
- 해당 차원의 모든 벡터가 벡터의 합과 스칼라-곱으로 표현될 수 있는 벡터의 조합을 를 기저벡터라고 한다.
벡터의 내적

- a,b가 단위 벡터라면, 내적의 결과는 코사인세타(cos) 이므로 범위는 -1 ~ + 1 이다 결과는 스칼라값
$$ a \cdot b = ㅣaㅣㅣbㅣ cos \theta $$
- 위 관계로 벡터의 크기(의 제곱)는 내적을 사용해서 다음과 같이 구할 수 있다.
$$ㅣaㅣ^2 = a \cdot a $$
벡터의 정규화
- 기준개념을 만들겟다?
- 벡터를 벡터 크기로 나누어 크기가 1인 단위벡터로 만다는 것
$$ㅣaㅣ^2 = a \cdot a $$
정규화를 하면,
$$ {a \over ㅣaㅣ} = {a \over \sqrt{ a \cdot a} }$$
- 크기가 0인 벡터는 정규화 할 수가 없다.
- 벡터를 벡터의 크기로 나눈다?
법선 벡터
- 평면에 수직이며, 크기가 1인 벡터
투영 벡터
- 벡터를 분해하고 각각 축의 벡터?
- * ${(a \cdot n) * n}$


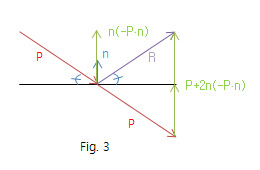
반사벡터
- 벡터가 평면에서 그대로 튀어 올랐을 떄의 벡터
- 입사각과 반사각이 동일한것
- 가는 투영벡터 ((a⋅n)⋅n(a⋅n)⋅n) 를 2를 곱해여 빼준다
- a−2(a⋅n)⋅n

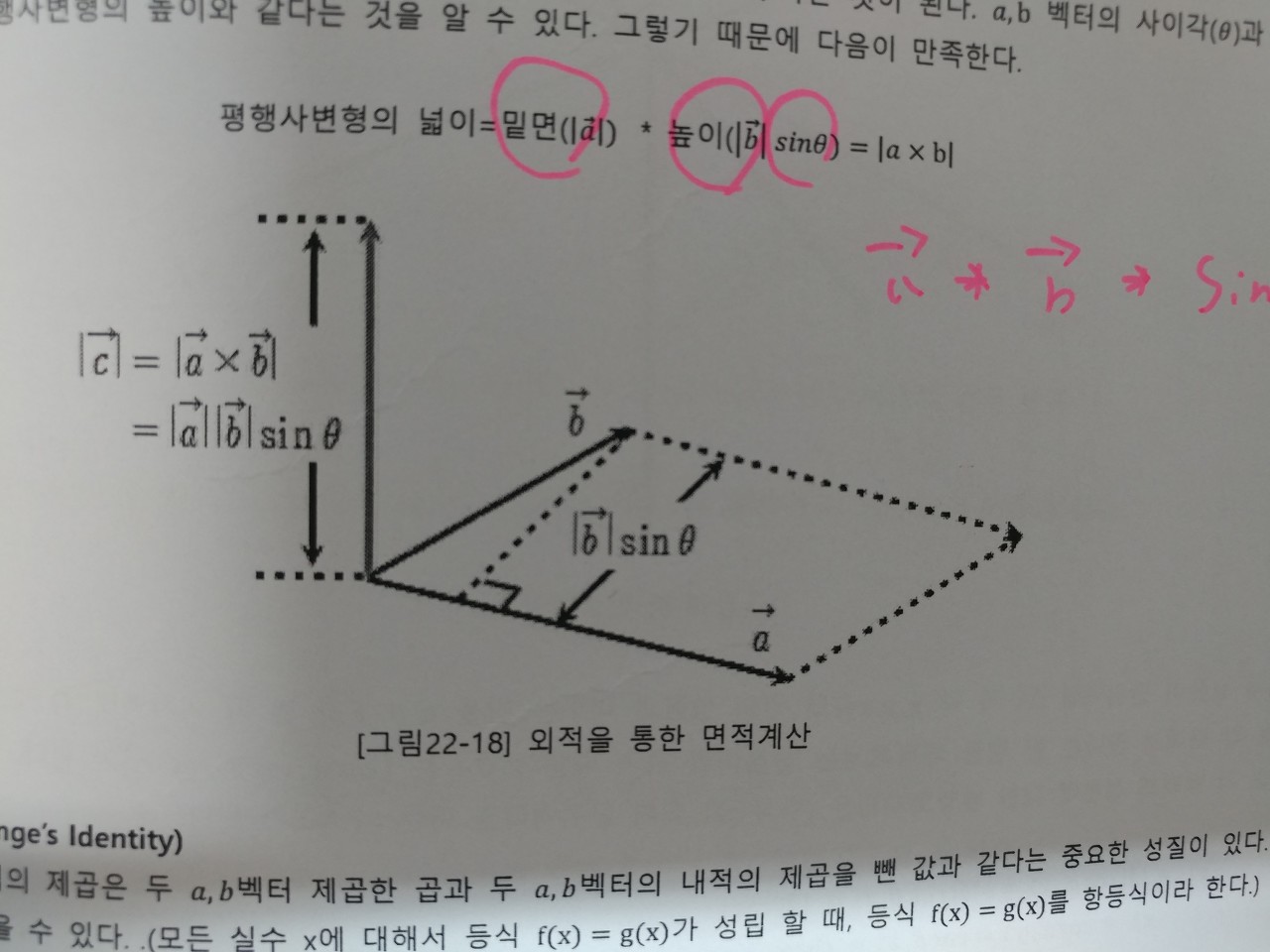
벡터의 외적
- 두 벡터의 수직인 벡터를 구한다
- 벡터의 순서를 바꾸면, 생성되는 벡터의 방향이 반대가 된다. 즉 벡터의 부호가 바뀐다.
- A×B=ㅣaㅣㅣbㅣsinθA×B=ㅣaㅣㅣbㅣsinθ
- A×AA×A 한개의 값으로 외적을 구하면 그 값은 0
- A⋅A×B=0,B⋅A×B=0A⋅A×B=0,B⋅A×B=0 외적벡터와 원래벡터의 내적은 0
- A×B×C=B(A⋅C)−A(B⋅C)
접선벡터
- 기저벡터의 일종
- 기저벡터와는 다르게 벡터의 방향이 변한다.
- 장소에 따라 방향이 바뀌는 기저벡터
- 노말방향(법선벡터)에 빛()
- 위도=θ,경도=ϕ위도=θ,경도=ϕ
- 법선 벡터 n=(cosϕcosθ,cosϕsinθ,sinϕ)n=(cosϕcosθ,cosϕsinθ,sinϕ)
- 정규화된 종법선 벡터 b=(−sinθ,cosθ,0)b=(−sinθ,cosθ,0)
- 접선벡터는 법선벡터와 종법선벡터에 직교 t=n×b

직교 기저
- 모든 벡터가 직교하는 기저를 직교 기저라고 한다
1 파이 : 180도
'수학' 카테고리의 다른 글
| 게임수학 개요 (0) | 2021.05.25 |
|---|---|
| 지수,로그 + 지수함수,로그함수 (0) | 2019.06.04 |
| 사원수 회전을 행렬로 (0) | 2019.05.01 |
| 사원수 (0) | 2019.05.01 |
| 행렬 (0) | 2019.05.01 |